[DreamHack] 01. LEVEL1 > chinese what?

문제 설명
CRT는 rsa에 많이 응용되는 정리입니다.
간단한 문제를 풀어보며 CRT란 무엇인지 알아보세요
문제 풀이
문제 풀이를 위해 파일을 받으면 output과 파이썬 실행 파일이 있다.

중국인의 나머지 정리(Chinese Remainder Theorem, CRT) 정리로 해당 플래그를 찾을 수 있다.
from Crypto.Util.number import long_to_bytes
from sympy.ntheory.modular import crt
# 주어진 소수와 나머지 값
p1 = 1527207470243143973741530105910986024271649986608148657294882537828034327858594844987775446712917007186537829119357070864918869
p2 = 2019864244456120206428956645997068464122219855220655920467990311571156191223237121636244541173449544034684177250532278907347407
p3 = 1801109020443617827324680638861937237596639325730371475055693399143628803572030079812427637295108153858392360647248339418361407
c1 = 232762450308730030838415167305062079887914561751502831059133765333100914083329837666753704309116795944107100966648563183291808
c2 = 869189375217585206857269997483379374418043159436598804873841035147176525138665409890054486560412505207030359232633223629185304
c3 = 1465704473460472286244828683610388110862719231828602162838215555887249333131331510519650513265133531691347657992103108331793683
# 중국인의 나머지 정리를 이용하여 원래 값을 복원
moduli = [p1, p2, p3]
remainders = [c1, c2, c3]
flag_recovered = crt(moduli, remainders)[0]
# 복원된 값을 바이트 문자열로 변환
flag_bytes = long_to_bytes(flag_recovered)
print(flag_bytes)
해당 코드 실행 시 플래그를 얻을 수 있다.
중국인의 나머지 정리 (Chinese Remainder Theorem, CRT) 란 ?

수론에서 중요한 정리 중 하나로 서로소인 여러 모듈러 연산의 결과로부터 원래의 수를 복원할 수 있게 해준다.
서로소인 n1,n2,...,nkn_1, n_2, ..., n_k

여기서 각 ni는 서로소여야한다.

위와같은 시스템이 주어질 때 n1,n2,...,nk가 서로소라면 x는 N= n1×n2×...×nk에 대해 모듈러 N에서 유일한 해를 갖는다. x≡1(mod3),
x≡2(mod5),
x≡3(mod7)
을 만족하는 x를 구하는 문제에서 시작된 정리이다.
(3으로 나누었을 때 나머지가 1이고, 5로 나누었을 때 나머지가 2이며, 7로 나누었을 때 나머지가 3인 수를 구하는 문제)
- 여기서 3, 5, 7은 "쌍마다 서로소"이다.
(3과 5는 서로소이고, 5와 7은 서로소이며, 3과 7은 서로소이다.)
Usage of CRT (중국인의 나머지 정리 활용 예시)
해당 시스템에 만족하는 x를 찾아야한다.
- 전체 모듈러 구하기
각 방적식의 모듈러를 곱하여 전체 모듈러를 구한다.
N = 3 x 5 x 7 = 105
- 각 Ni 구하기

- 각 Mi 구하기
35를 3으로 나눈 나머지를 찾으면: 35 ≡ 2 (mod 3)
즉 35의 나머지 2⋅M1≡1(mod3) 이 식이 성립된다.
따라서 M1은 M1
M1이 2가 되는 이유는 2 ⋅ 2 = 4 ≡ 1 ( mod 3 )이기 때문
- N2와 M2
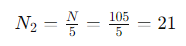
21의 모듈로 5에 대한 역원 M2를 찾는다 : 21 ⋅ M2 ≡ 1 ( mod 5 )
21을 5로 나눈 나머지를 구하면 : 21 ≡ 1 ( mod 5 )
즉 21의 나머지 1 ⋅ M2 ≡ 1 ( mod 5 ) 이 식이 성립된다.
따라서 M2 = 1
- N3와 M3
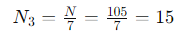
15의 모듈로 7에 대한 역원 M3를 찾는다 : 15 ⋅ M3 ≡ 1 ( mod 7 )
15를 7으로 나눈 나머지를 구하면 : 15 ≡ 1 ( mod 7 )
즉 15의 나머지 1 ⋅ M3 ≡ 1 ( mod 7 ) 이 식이 성립된다.
따라서 M3 = 1
- 계산하기
각 방정식을 통합하여 x값을 구한다.
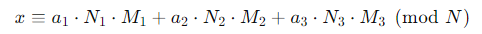
여기서 a1 = 2, a2 = 3, a3 = 2
따라서
x ≡ 2 ⋅ 35 ⋅ 2 + 3 ⋅ 21 ⋅ 1 + 2 ⋅ 15 ⋅ 1 ( mod 105 )
x ≡ 140 + 63 + 30 ( mod 105 )
x ≡ 233 ( mod 105 )
233을 105로 나눈 나머지 값을 구하면 233 ≡ 23 ( mod 105 )
따라서 x ≡ 23 ( mod 105 )
